矩阵的秩是什么意思（矩阵的秩与解的运算关系）

什么是矩阵的秩？

前面我们介绍了矩阵的基本概念，请参见矩阵的基本知识。 也讲了高斯消元法解线性方程组，请参考用高斯消元法解决线性系统问题。

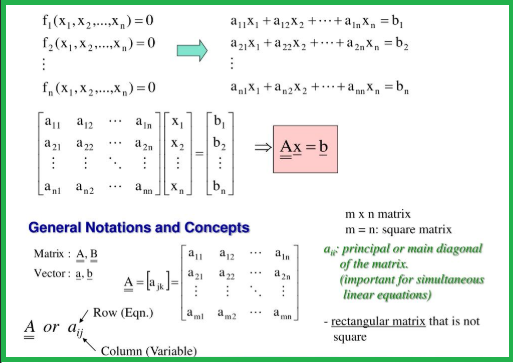
本文谈谈矩阵秩的概念，先看一个例题：解下列线性方程组的解，

我们按高斯消元法，首先列出增广矩阵：

第2行减去第1行的两倍，第3行减去第1行得到：

现在第三行减去第二行(注意只能先消去下面的行)，然后把第二行乘以1/3（第二行的操作不能让别的行对其运算，否则再乘以1/3没有意义）:

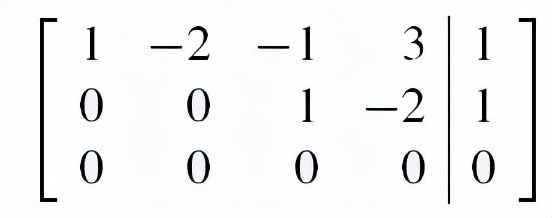
这是行阶梯形，我们通过把第二行加到第一行来把它化简（只能从下往上运算）：

相应的简化方程组为：

首非零元为1在第1列和第3列，所以对应的变量

和

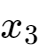
被称为首变量（主要的变量），因为矩阵是行最简阶梯形，所以这些方程可以用系数非1变量

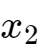
和

来解首变量，即把

,

看成变量。更准确地说,在这个例子中，我们设

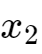
= s和

= t，其中s和t是任意的，所以这些方程变成

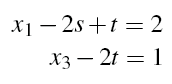
最后方程组的解用参数s, t表示变成：

由于s, t是任意数，所以这个方程组有无穷解，上述过程中我们用了反代方法，即把x4当做已知的参数t, 然后带入第三个方程，依次类推，得出每个变量，这种方法叫反代法。

那么问题是什么时候方程组有唯一解，什么时候方程组有无数解，什么时候方程无解？这就要引出秩（rank）的概念。

秩的定义：矩阵A的秩是任意矩阵A经过行变换化成阶梯矩阵后，行的首元为1的个数。

例题：求矩阵A的秩。

解：按照高斯消元法，将矩阵A化为行的阶梯矩阵有，

因为行的阶梯矩阵首元为1共有两个，所以r=2.

假设矩阵A是mxn矩阵， 即有m行和n列。那么r≤m是因为首元1位于不同的行中，同理r≤n，是因为首元1位于不同的列中。此外, 秩对判断方程组的解有很好的应用。

下面给出方程组解的判定。

定理：假设一个包含n个变量的m个方程的所构成的方程组是有解的，并且其增广矩阵的秩是r， 那么：

1.解的恰好包含n - r个参数。

2.如果r <n，方程组有无穷多个解。

3.如果r = n，方程组有唯一解。

证明：增广矩阵的秩是r的事实意味着正好有r个主变量（系数为1的变量），因此正好有n - r个非主变量。这些非主元变量都作为参数赋值，所以解的恰好包含n - r个参数。因此，如果r <n，至少有一个参数，因而有无穷多个解。如果r = n，没有参数，所以是唯一解。

这个定理有三个含义：

1. 没有解的情况。当一行出现［ 0 0··· 0 1 ］以行梯队形式出现时，就会发生这种情况。这是方程组无解的情况。

2. 唯一的解。当每个变量都是主元变量时，就会发生这种情况。

3.无穷多的解。当系统是一致的并且至少有一个非主元变量时，就会发生这种情况，因此至少有一个参数。

最后再看一个例子，解方程组：

解：增广矩阵经过初级行变换为：

这样意味着方程组变换为：

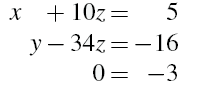
这是一个与原方程组等效的方程组，但最后一个意味着0x+0y+0z = −3, 所以无解。

总结：若解一个线性方程组有下列步骤,

1. 做方程组系数和常量组成的增广矩阵，

2. 将增广矩阵化简为行阶梯矩阵，

3. 观察最后一行或其他行有无出现无解的行，若有则方程组无解，

4. 若有解利用上面解的判定定理确定解的个数，

5. 若有唯一解，可直接求出，

6. 若有无穷解，用参数形式解出，此时参数的个数为n-r, 即有n-r个的变量参数。